Concepts

The simplified model: without tracing

The confidential transfer in Findora has a comprehensive support of tracing, which enables an asset tracer to see information in a confidential transfer, depending on the tracing policy, the amount, the asset type, and/or the sender's identity and attributes.

To get started, we focus on the simplified model where tracing is removed. This allows us to focus on Bulletproofs and Ristretto ciphertexts.

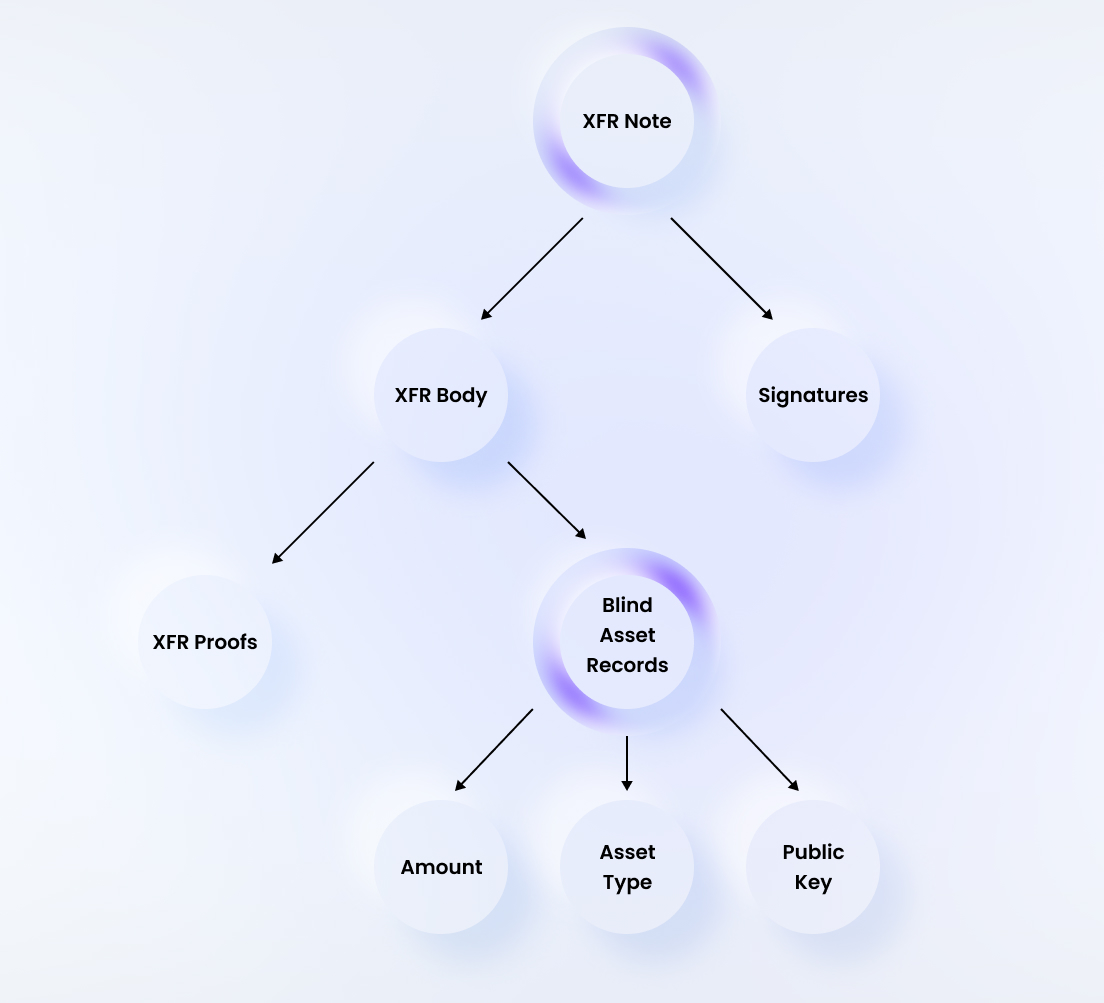
Note (layer 1): A note consists of a body and a list of signatures by the senders over the body. An asset transfer is executed simply by posting a transfer note to the Findora ledger, denoted XfrNote for short.

pub struct XfrNote {
    pub body: XfrBody,
    pub multisig: XfrMultiSig,
}

Body (layer 2): A body consists of (1) blind asset records for inputs, (2) blind asset records for outputs, (3) a proof about the amounts and the asset types, and (4) owner memos.

pub struct XfrBody {
    pub inputs: Vec<BlindAssetRecord>,
    pub outputs: Vec<BlindAssetRecord>,
    pub proofs: XfrProofs,
    pub asset_tracing_memos: Vec<Vec<TracerMemo>>, // each input or output can have a set of tracing memos
    pub owners_memos: Vec<Option<OwnerMemo>>,
}

Blind asset record (layer 3): A blind asset record consists of three parts: (1) amount, (2) asset type, and (3) owner address. Here, the amount and the asset type can be either confidential or public. When it is confidential, it is in the form of a Ristretto commitment of the corresponding information. When it is public, it is the original information as it is.

pub struct BlindAssetRecord {
    pub amount: XfrAmount,        // Amount being transferred
    pub asset_type: XfrAssetType, // Asset type being transferred
    pub public_key: XfrPublicKey, // ownership address
}

Amount and asset type proof (layer 3): A zero-knowledge proof that certifies that the blind asset records of inputs and of outputs are matching. It has five possibilities:

• Public amount, public asset type:

  • A proof is not necessary.

• Confidential amount, single public asset type:

  • A Bulletproof for (1) all the output amount commitments and (2) the accumulated input commitment subtracted by the accumulated output commitment. The proof shows that these commitments contain values within the range $[0, 2^{32})$.

• Single confidential asset type, public amount:

  • A delegated Schnorr proof that shows that all the input and output commitments are for the same asset type.

• Confidential amount, single confidential asset type:

  • A Bulletproof as above.
  • A delegated Schnorr proof as above.

• Multiple assets:

  • An asset mixing proof over all the inputs and all the outputs, see below.

Owner memos (layer 3): The owner memo is an encryption of the secret information necessary for the recipient to spend the assets. The owner memo consists of two parts:

• a random point on the elliptic curve, used to derive the same amount and asset type blinding factors for the recipient, through the Diffie-Hellman key exchange.

• a standard Ed25519 hybrid encryption ciphertext, which encrypts the amount and the asset type, through Diffie-Hellman key exchange and AES-256-CTR.

Note that if the transaction only hides the amount, then the owner memo will only encrypt the amount. Same for the asset type. If the transaction is transparent, i.e., not hiding any amount or asset type information, then the owner memo will not appear.

Range proof

The range proof works as follows. Let us assume that each of the input assets and output assets are represented in terms of two commitments, one representing the higher $32$ bits of the amount, one representing the lower $32$ bits. If some of the assets have a transparent amount, we convert it into a commitment with dummy blinding (i.e., the blinding factor is zero).

Prover: The prover wants to demonstrate the following range claims:

• The two commitments (high and low) of each of the output assets are committing a value in $[0, 2^{32})$.

• Compute the sum of all the input amounts subtracted by the sum of all the output amounts. This should be a value in $[0, 2^{32})$. If this value is not zero, it means that this confidential transfer has burnt some tokens into the thin air. Extract the high 32-bit and low 32-bit of this value, denoted by $a$ and $b$ accordingly.

• Compute the sum of all the input blinding factors for the low parts subtracted by the sum of all the output blinding factors for the low parts, denoted by $c$. Do the same for the high parts, denoted by $d$.
• Create a commitment with value $a$ and blinding factor $c$, denoted by $C_1$. Create another commitment with value $b$ and blinding factor $d$, denoted by $C_2$.

Verifier: The verifier first computes the sum of all input commitments for the low parts subtracted by the sum of all output commitments for the low parts, denoted by $C_3$. Do the same for the high parts, denoted by $C_4$. These two commitments are ``similar'' to the ones that the prover constructs. The verifier checks as follows:

$C_1 + 2^{32}\cdot C_2 \stackrel{?}{=} C_3 + 2^{32}\cdot C_4$

Then the verifier verifies the range claim against all the output commitments as well as $C_1$ and $C_2$. If the proof passes, it means that the all the output commitments are committing a number in $[0, 2^{32})$, and that the sum of the input amounts subtracted by the sum of the output amounts is nonnegative.

Mixing proof

The mixing proof checks if the inputs and the outputs are matching. Different from the range proof, the mixing proof is able to handle different asset types.

The mixing proof uses the Bulletproofs-based mixing protocol, which is part of the Zei library and is documented in the Cryptography Module.

The complete model: with tracing

We now describe the complete model of confidential transfer, which additionally includes asset tracing proofs and tracer memos. These two are corresponding to the tracing policies of a given asset. We now describe these three structures.

Asset tracing proofs

The asset tracing proofs are used to show that the tracer memos, which encrypt information about the transaction, match what is exactly in the transaction. It consists of three parts.

• Asset type and amounts proofs:

  • For each tracer key, there would be an aggregated proof for the equality of the Pedersen commitments of asset types and amounts and their ElGamal ciphertexts.

• Input identity proofs:

  • If the asset's tracing policy requires identity tracing, the proof here shows that the encrypted attributes are correct attributes of the users associated with the inputs. If the tracing policy does not require it, then these proofs are omitted.

• Output identity proofs:

  • Similar to input identity proofs.

Tracer memos

For each record with confidential amount or asset type, and for each tracer of this asset, there is a tracer memo that provides information about the transaction as well as identity information about the sender and the recipient. Each tracer memo consists of the following parts.

• Encryption keys:

  • Used for the tracer to identify memos that direct to them. It includes three different keys.

    • Record data encryption key: ElGamal encryption key for the amount and asset type. It has to be ElGamal encryption in order to enable asset type and amounts proofs.
    • Attributes encryption key: Also ElGamal encryption key, but for the attribute information. It has to be ElGamal encryption in order to enable input and output identity proofs.
    • Lock information encryption key: A hybrid encryption key that encrypts all the information above, for a quick reference, but there are no proofs that certify its equivalence.

• Locked amount:

  • If the amount is encrypted, it stores a ciphertext for the higher 32 bits of the amount, and a ciphertext for the lower 32 bits of the amount.
  • This field is optional.

• Locked asset type:

  • If the asset type is encrypted, it stores a ciphertext for the asset type.
  • This field is optional.

• Locked attributes:

  • A list of encrypted attribute information.

• Locked info:

  • A hybrid encryption ciphertext for all the plaintexts appearing in the ciphertexts above.